Programm
Contour
Voraussetzung:
Betriebssystem Windows 95 oder höher
Programmgröße 96 KBytes
Programmentwicklung
Dr. Ing. Ulrich Röhr
22117 Hamburg
Glitzaweg 17a
Tel: 040/7126833
Übersicht
1.Wozu dient das Programm
2.Programmanwendung
3.Aufbau der Eingabedatei
4.Ergebnisse
5.Daten speichern
6.Daten einlesen
7.Berechnungsgrundlagen
8.Tastenbelegung
1.Wozu dient das Programm?
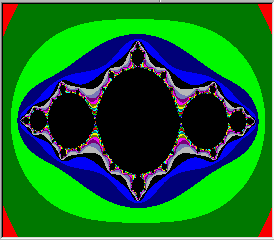
Das Programm berechnet aus vorgegebenen Höhenangaben d.h. Z-Werten, eine Oberfläche und bildet sie mit Höhenlinien ab. Die Z-Werte gehören zu einer Grundfläche, die über X- und Y- Koordinaten beschrieben wird.
Die einzelnen Werte der Oberfläche können in der Grafik abgefragt werden und werden in der Statuszeile angezeigt. Ein ausgewählter Bildausschnitt kann auch vergrößert werden. Ebenso sind Extrapolationen außerhalb der vorgegebenen Grundfläche möglich.
Das Programm ermöglicht damit Verteilungskarten, z.B.:
Mächtigkeitsverteilung
Porositätsverteilung
Permeabilitätsverteilung
Allgemeine Oberflächen
2.Programmanwendung.
für die Anwendung wird folgendes Vorgehen vorgeschlagen:
1.Start des Programmes
2.Aufbau einer Eingabedatei bzw.
3.Einlesen einer Eingabedatei
4.Ansicht der Ergebnisse
5.Ausschnittsbetrachtung
6.Abspeichern der Eingabedaten
7.Programm beenden
Nach dem Programmstart erscheint das Hauptfenster mit einer Menüleiste, die folgende Auswahl bietet:
DATEI BEARBEITEN ANSICHT ?
 |
Abb.1 Menüleiste mit Symbolleiste
Zuerst wird eine Eingabedatei aufgebaut oder eine bereits vorhandene Eingabedatei gelesen.
Diese 3 spaltige Datei besteht aus X-Werten, Y-Werten und Z-Werten.
Dann wird die Berechnung durchgeführt bzw. die Berechnung mit geänderten Daten wiederholt. Die Ergebnisse stehen in Tabellenform als Textansicht oder auch als Grafik zur Verfügung.
3. Aufbau der Eingabedatei
Über die Menüauswahl BEARBEITEN- DATEN ÄNDERN oder über DATEI- NEU wird ein Eingabedialogfenster geöffnet. Die Auswahl kann auch über das Kontextmenü getroffen werden, das mit der rechten Maustaste aufgerufen wird. Über dieses Dialogfenster können die Daten eingegeben und verändert werden.
Für den ersten Dateiaufbau wird folgendes Vorgehen vorgeschlagen:
1. Eingabe des Titels
2. Festlegung des Polynomgrades für die mathematische Annäherung
3. Eingabe der X-,Y- und der Z-Werte
Die Eingabe kann auch über das Einlesen einer Datei erfolgen Dazu ist die TASTE DATEI ÖFFNEN zu drücken. Die 1. Zeile der eingelesenen Fremddatei wird als Titelzeile aufgefaßt.
Die 2. Zeile wird als Kommentar überlesen. Die folgenden Zeilen müssen jeweils 3 Werte enthalten, den X- Wert, den Y- Wert und den Z- Wert.
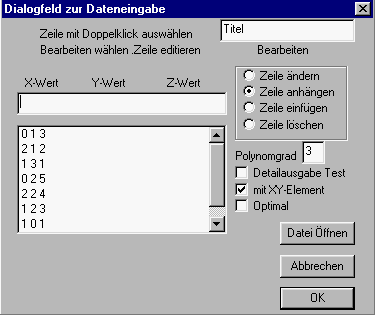 |
Abb.2 Dialogfeld zur Dateneingabe
Wenn die Eingabe mit OK verlassen wird, werden die Daten gespeichert und die Berechnung wird durchgeführt. Die Ergebnisse stehen in Tabellenform und als Grafik zur Verfügung, je nachdem welche Auswahl im Menü getroffen wurde. ANSICHT- GRAFIK zeigt die Ergebnisse als Grafik, ANSICHT- TEXTANSICHT zeigt die Ergebnisse in Tabellenform.
Wenn das Dialogfeld zur Dateneingabe über die TASTE ABBRECHEN verlassen wird, werden keine Änderungen in der Eingabedatei gespeichert.
4.Ergebnisse
Die Berechnung wird durchgeführt, wenn der Dialogfeld über die OK- TASTE
verlassen wird. Die Ergebnisse liegen in Textform oder als Grafik vor. Unter ANSICHT
Kann zwischen TEXT und GRAFIK gewählt werden. Unter ANSICHT können auch die EINGABEDATEN ebenso wie die ERGEBNISSE gewählt werden.
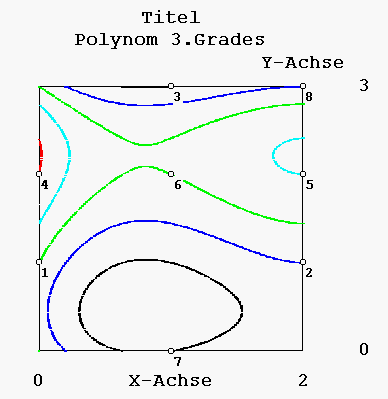 |
Abb. 3 Beispiel einer Oberfläche
In diesem Beispiel wurden 8 Punkte mit X- Werten, Y- Werten und Z- Werten vorgegeben. Die schwarze Kurve mit dem Z- Wert=1 geht durch den Punkt 7. Die zur Oberfläche gehörende Legende zeigt Abb.4.

Abb.4
Legende zu Abb.3
Die einzelnen Werte können auch in der Grafik abgefragt werden und in der Statuszeile angezeigt werden. Dazu ist der MAUSZEIGER an die entsprechende Stelle zu führen und die LINKE MAUSTASTE zu drücken. Der X-Wert, der Y-Wert und der Z-Wert werden in der Statusleiste angezeigt.
Der gewünscht Bildausschnitt kann auch verändert werden. Über ANSICHT ZOOM wird ein Dialog geöffnet, über den der minimale und maximale X- und Y-Wert festgelegt werden können.
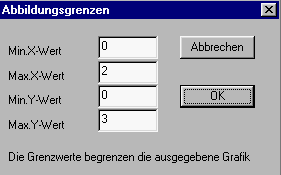 |
Abb.5 Neue Abbildungsgrenzen
Zur ursprünglichen Ansicht kommt man wieder über DATEN ÄNDERN OK.
Bei der Grafik ist die Breite und die Höhe jeweils 14 cm. Damit ergeben sich unterschiedliche Maßstäbe für die X-Achse und die Y-Achse. Ein einheitlicher Maßstab kann dadurch eingestellt werden, daß die Differenz Max. X-Wert – Min. X-Wert genauso groß gewählt wird wie Max. Y-Wert - Min. Y-Wert.
Alle Ergebnisse können auch über den Drucker ausgegeben werden mit der Wahl DATEI- DRUCKEN. Oder sie können zuvor in der SEITENANSICHT angesehen werden. Beim Wechsel von Hochformat auf Querformat muß DRUCKER EINRICHTEN gewählt werden.
Mit der rechten Maustaste wird ein Kontext-Menü ausgelöst, das folgende Auswahlmöglichkeiten anbietet:
DATEN ÄNDERN
TEXTANSICHT
GRAFIK
DATEI NEU
DATEI ÖFFNEN.
Mit diesem Kontext Menü kann genau wie mit dem Hauptmenü gearbeitet werden.
5.Daten speichern
Beim Verlassen des Programmes können die Eingabedaten unter einem beliebigen Dateinamen gespeichert werden. Bei Änderung der Daten wird gefragt ob die Daten gespeichert werden sollen.
Mit der Menüauswahl DATEI SPEICHERN oder SPEICHERN UNTER wird der Dateiname festgelegt. In dieser Datei werden die Eingabedaten abgespeichert.
6.Daten einlesen
Eingabedaten, die zuvor abgespeichert wurden, können wieder eingelesen werden. Dazu wählt man DATEI- ÖFFNEN und wählt die entsprechende Datei aus. Die Auswahl ist auch über das Kontextmenü möglich, das über die rechte Maustaste geöffnet wird.
7.Berechnungsgrundlagen
Berechnung
Von den eingegebenen Daten wird entsprechend des gewählten Polynomgrades eine Grundmatrix aufgestellt. Das Lösungspolynom z.B. 3.Grades lautet dann
Z = a +b*x + c*x^2 + d*x^3 + e*y +f*y^2 + g*y^3
Hiebei sind a bis g die gesuchten Lösungskoeffizienten.
Zu Beginn wird folgende Grundmatrix aufgestellt:
MAX Sx Sx2 Sx3 Sy Sy2 Sy3 = Sz
Sx Sx2 Sx3 Sx4 Sxy Sxy2 Sxy3 = Szx
Sx2 Sx3 Sx4 Sx5 Sx2y Sx2y2 Sx2y3 = Szx2
Sx3 Sx4 Sx5 Sx6 Sx3y Sx3y2 Sx3y3 = Szx3
Sy Syx Syx2 Syx3 Sy2 Sy3 Sy4 = Szy
Sy2 Sy2x Sy2x2 Sy2x3 Sy3 Sy4 Sy5 = Szy2
Sy3 Sy3x Sy3x2 Sy3x3 Sy4 Sy5 Sy6 = Szy3
Hiebei bedeutet Sx4 Summe aller x^4 und Syx2 Summe aller y*x^2.
Nach dem Eliminationsverfahren Gauß Jordan wird die Einheitsmatrix als Lösungsmatrix entwickelt und so die Lösungskoeffizienten bestimmt
1 0 0 0 0 0 0 = a
0 1 0 0 0 0 0 = b
0 0 1 0 0 0 0 = c
0 0 0 1 0 0 0 = d
0 0 0 0 1 0 0 = e
0 0 0 0 0 1 0 = f
0 0 0 0 0 0 1 = g
Wählt man bei der Dateneingabe mit XY Element ,so wird ein Polynom mit einem
X*Y- Element gesucht. Für ein Polynom 3.Grades lautet die Lösung:
Z = a +b*x + c*x^2 + d*x^3 +e*x*y + f*y +g*y^2 + h*y^3
Hiebei müssen 8 Koeffizienten bestimmt werden, d.h. es sind mindestens 8 Eingabepunkte für eine Lösung erforderlich. Für weniger Punkte muß ein kleinerer Polynomgrad gewählt werden. Um die Rechengenauigkeit zu verbessern ,werden die X- oder Y-Werte- wenn sie größer als 100 sind durch einen Faktor wie 100 oder 1000 geteilt. Dieses Vorgehen wird angezeigt.
8.Tastenbelegung
1.Die Taste F1 ruft die Hilfe auf.
2.Die Taste F2 ruft das Dialogfeld DATEN ÄNDERN auf.
3.Die ESCAPE –Taste führt beim Eingabedialog zum Abbruch
4.Die SHIFT- Taste bewegt den CURSOR im Dialogfeld